一直没更博客,被大佬吐槽说是不是鸽了
确实是咕咕咕了好久(
惯例的习题答案
数据抽象导引
见:数据抽象导引
层次性数据和闭包性质
序对为我们提供了一种构造复合数据的基本“粘接剂”。利用cons,我们不仅可以组合起各种数值,更可以组合起各种序对。
我们将这种能力称为cons的闭包性质,即通过它组合数据对象得到的结果本身,还可以通过同样的操作再次组合。基于此,我们可以建立起一个层次性的结构用来表示各种复杂的复合结构。
序列的表示与层次性结构
利用序对可以构造出的最常用的结构即是序列,我们可以将序列表示为序对的链:
(cons 1 (cons 2 (cons 3 (cons 4 nil))))
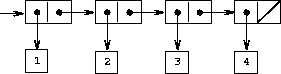
图1 将序列1,2,3,4表示为序对的链1
这样的序对的序列称为一个表,上述过程也可以简写成(list 1 2 3 4),它返回表(1 2 3 4)
将表的表示推广到元素本身也是序列的序列,我们可以进一步地得到更复杂的结构,如树:
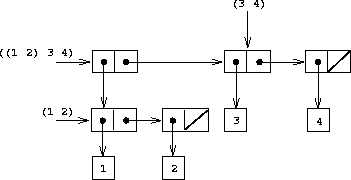
图2 由(cons (list 1 2) (list 3 4))形成的结构2
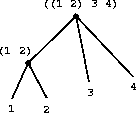
图3 将图2中的表结构看作树3
在表的基础上,car可以解释为取表的第一项,cdr可以解释为取表的余下项构成的子表,而cons则可以解释为连接元素与表,利用他们我们便可以构造出更多的表操作。
一个很有用的操作是将某种变换应用于表中各个元素,然后得到结果构成的表,且元素相对顺序不变,这一高阶过程称为map,举例来说:
(define (map proc items)
(if (null? items)
nil
(cons (proc (car item))
(map proc (cdr items)))))
(map abs
(list -1 2 -3 -4)) ; (1 2 3 4)
(map (lambda (x) (* x x))
(list -1 2 -3 -4)) ; (1 4 9 16)map将我们对元素的操作提升成了对表的操作,分离开了表内部结构的遍历过程、表的构造过程与对元素本身的映射过程,两个部分可以完全独立变化。
序列作为一种约定的界面
数据抽象的作用已在前文中提过,它使我们能够设计出各层相对独立,不会被不必要的数据表示细节纠缠的程序。
在这里,先考虑一下以下两个过程:
;; 计算树中值为奇数的叶子节点的平方和
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares (car tree))
(sum-odd-squares (cdr tree))))))
;; 构造出所有偶数的斐波那契数的表
(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))
(next 0))二者结构差异相当大,但他们计算过程却很相似。
sum-odd-squares:
- 枚举出树的树叶
- 过滤选出奇数
- 对选出的数各自求平方
- 初始值为0,用
+累积得到的结果
even-fibs:
- 枚举出0到n的整数
- 对得到的数求相应的斐波那契数
- 过滤选出偶数
- 初始值为空表,用
cons累积得到的结果
如果我们将这两个过程想象成两个信号处理系统,那么其各个步骤可以自然地抽象为枚举器、过滤器、映射器、累积器,如图:
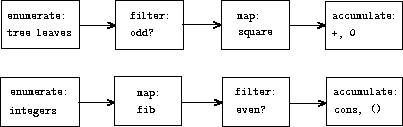
图4 两个过程的信号流图揭示出的共性4
但原始版本的过程过于深入数据结构的细节,将各个处理步骤混合在了一起,没有展现出这一信号流的结构,缺乏组织性。
如果我们能基于对数据流动的认识来组织程序,以更清晰地反应这些信号流的结构,我们的程序也可能会变得更为清晰。要做到这一点,最关键的就是将注意力放在处理过程中两个步骤之间流动的信号上。如果我们能统一这些信号的结构,比如用表来表示,那么我们就可以利用表操作实现各个步骤的处理。
改造后,两个过程的表示如下:
;; 计算树中值为奇数的叶子节点的平方和
(define (sum-odd-squares tree)
(accumulate +
0
(map square
(filter odd?
(enumerate-tree tree)))))
;; 构造出所有偶数的斐波那契数的表
(define (even-fibs n)
(accumulate cons
nil
(filter even?
(map fib
(enumerate-interval 0 n)))))将程序表示为一些针对序列的操作,我们可以得到一些较为独立的片段,做到模块化的程序设计。
在这里,序列成为了一种约定的界面,统一了各个模块之间的接口。通过重用组合这些使用了约定界面的模块,我们可以得到清晰而灵活的程序。
强健的语言层次
由过程抽象与数据抽象的关键思想,我们可以认识到程序设计的另一个关键概念,即分层设计:一个复杂的系统应由一系列的层次构造出来,为了描述这些层次,需要使用一系列的语言。
构造各个层次的方式,就是使用这一层次中的各种基本元素与组合手段,抽象掉该层次的部分细节,构造出一些这一层次的基本部件。这样构造出来的部件又可以作为另一个层次里的基本元素。每一层都为系统在某一特征上提供一套独特的描述与处理方式,一层一层地设计组合来得到最终的系统。
分层设计使得我们的程序变为强健的多个层次,我们可以在需要变更时只修改当前层而不影响到其他层,也可以在高层处理高层的问题而不牵扯到底层实现。
这种方法在复杂的系统中被广泛使用,如计算机的层次结构:从使用模拟电路语言构造出的门电路,到更上一层数字电路语言构造出的运算器、总线、接口电路,一步一步地构造出了一个计算机。而各个计算机本身也可以作为一个巨大的分布式系统的一部分,使用网络通信相关的语言构成一个集群。
符号数据
见:符号数据
抽象数据的多重表示
带有通用型操作的系统
待续